Отдел сверхпроводящих и мезоскопических структур

Главное меню:

Исследования

С. И. Бондаренко (рук. группы), В. П. Коверя, А. В. Кревсун, В. П. Тимофеев

Квантовые интерференционные структуры для исследования энергетической щели

и времени релаксации сверхпроводящего состояния

Вступление

Энергетическая щель (Δ) сверхпроводника и время релаксации (τ) сверхпроводящего состояния являются ключевыми параметрами сверхпроводников. Энергетическая щель определяет, в частности, максимально возможную скорость перемещения куперовских пар и плотность критического тока сверхпроводника. Время релаксации определяет максимальную скорость быстродействия устройств на основе сверхпроводников. Минимизация этого параметра способствует развитию высокочастотных и слаботочных сверхпроводящих устройств для современной СВЧ и вычислительной техники.

Основные положения метода

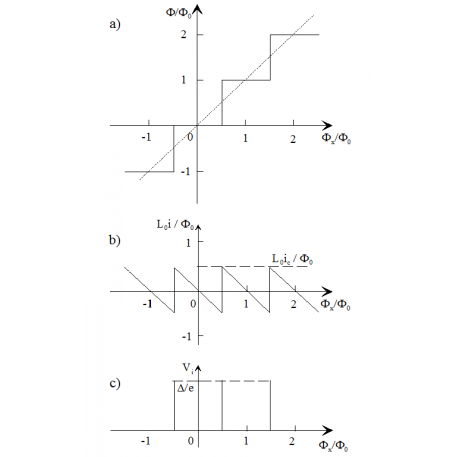
Мы предложили и исследовали новый метод, который позволяет проводить одновременные измерения щели и времени релаксации. Метод объединяет две базовых концепции. Первая из них есть теоретическое предсказание Сильвера и Циммермана о том, что импульсное напряжение V_i на сверхпроводящем квантовом интерферометре (СКИ) во время дискретного переключения циркулирующего тока i в нем, вызванного изменением магнитного потока Ф_x, пропорционально энергетической щели сверхпроводника (Рис.1). Второй из них являются наши предложения о продлении длительности импульса к хорошо измеряемой величине путем шунтирования интерферометра сверхпроводящей катушкой с большой индуктивностью L ≈ L₃ + L₄ , которая существенно превышает индуктивность L₀ интерферометра (Рис.2).

Рис.1 Расчетная зависимость относительного внутреннего магнитного потока Ф/Ф₀ (a), относительного циркулирующего тока L₀i /Ф₀ (b) и импульсного напряжения V_i (c) от относительного внешнего магнитного потока Ф_х/Ф₀ , накладываемого на интерферометр с индуктивностью L₀. Зависимости получены Сильвером и Циммерманом в линейном приближении при условии i_с ≈ Ф₀ /(2L₀), Ф₀ – квант магнитного потока.

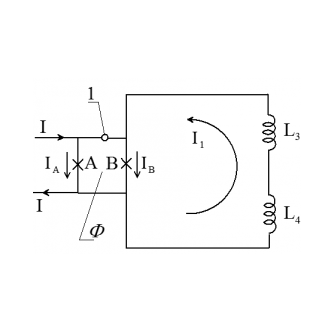
Рис.2 Электрическая схема модельного контура измерительного устройства, в котором прижимный точечный контакт (ПТК) представлен в виде асимметричного СКИ (1) с двумя микроконтактами A и В, имеющими разные критические токи и включенными в ветви с разными индуктивностями, Ф - магнитный поток через контур СКИ.

Измерения

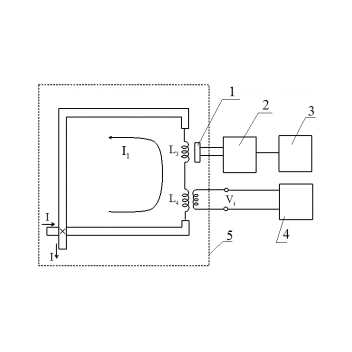
Схема экспериментальной установки для измерения щели и времени релаксации представлена на Рис.3.

Рис.3 Измерительная схема для изучения токовых состояний контура с ПТК в точке пересечения (х) ниобиевых микропроводов: I – транспортный ток, 1 – феррозондовый детектор для измерения магнитного поля тока I₁, протекающего через L₃ и L₄, 2 – усилитель сигнала детектора, 3 – регистратор величины измеряемого магнитного поля, 4 – осциллограф для визуализации и измерения импульсов напряжения V_i на вторичной обмотке трансформатора, вызванного дискретным изменением тока I₁ через первичную обмотку с индуктивностью L₄, 5 – криостат.

Прижимной точечный контакт (ПТК) ниобий - ниобий был использован в качестве интерферометра. Циммерманом с коллегами раньше было установлено, что микроструктура ПТК представляет собой квантовый интерферометр с несколькими параллельно соединенными микроконтактами. В частности, можно сделать ПТК с двумя микроконтактами. Такая структура представляет собой сверхпроводящий интерферометр постоянного тока (ПТ) и может быть чувствительным элементом, известным как ПТ СКВИД. ПТК получен путем механического сжатия двух наложенных друг на друга ниобиевых микропроводов диаметром 70 мкм. Ниобиевые провода образуют замкнутый сверхпроводящий контур в ПТК с индуктивностью L₀ около 10^-13 Гн. Другая часть контура состоит из двух катушек (L₃ и L₄), одна необходима для расположения в ней детектора феррозондового магнитометра (FG), а другая – для образования первичной обмотки импульсного трансформатора. Феррозонд служит для измерения тока в контуре. Трансформатор служит для регистрации импульса напряжения, возникающего в момент дискретного квантового перехода в интерферометре. Сначала постоянный ток I течет через ПТК, в то время как ток в ветви контура с индуктивностью 10^-6 Гн практически равен нулю. Интерферометр переходит в резистивное состояние с сопротивлением R за короткое время т ≈ L₀ / R , как только достигается его критический ток. Возникает импульс напряжения V_і на интерферометре и контуре, в то время как часть транспортного тока переключается в высокоиндуктивную часть контура, создавая ток I₁ за время δt ≈ L /R. Потом интерферометр возвращается в сверхпроводящее состояние. Новый дискретный переход может произойти в интерферометре после последующего увеличения транспортного тока I , создающего магнитный поток, равный кванту магнитного потока Ф₀ в интерферометре. В результате мы имеем зависимость тока в контуре I₁ от транспортного тока I , показанную на Рис.4а. Периодические ступени тока на зависимости I₁(I) отвечают квантовым переходам тока (i) интерферометра, шунтированного сверхпроводящей индуктивностью.

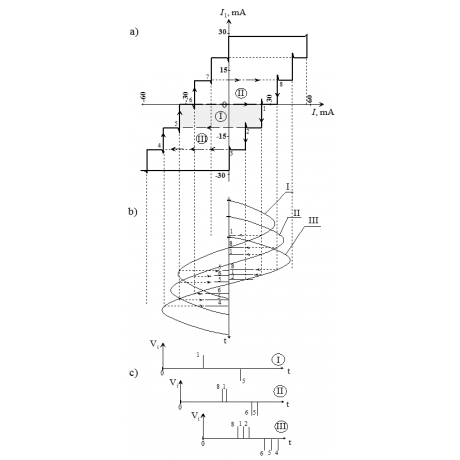
Рис.4 Схема получения различного количества импульсов напряжения V ^*_i₄, наблюдаемых на экране осциллографа, когда переменный транспортный ток пропускается через контур: а) начальная экспериментальная зависимость I₁ (I) при Т = 4.2К; b) изменение переменного тока на протяжении одного периода при трех различных его амплитудах I, II, III; с) картина импульсов напряжения на экране осциллографа (1-8 – номера ступеней тока I₁, которые возникают при различных амплитудах переменного тока).

Результаты

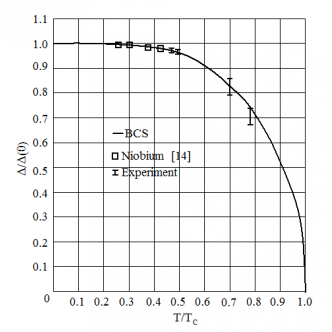
Развертка этой зависимости низкочастотным транспортным током (Рис.4b) позволяет наблюдать на экране осциллографа (Рис.4c) импульсы напряжения с длительностью , амплитуда которых отвечает энергетической щели ниобия, которая оказывается равной 2.3мВ при 4.2К. На рис.5 показанные экспериментальные значения щели и расчетной кривой температурной зависимости щели. Длительность квантового перехода в интерферометре, то есть время релаксации сверхпроводящего состояния в ниобии, может быть оценена из соотношения индуктивности интерферометра (L₀ = 10^-13 Гн) и контура (L = 10^-6 Гн):

τ ≈ (L0 / L) δt . (1)

Таким образом, как следует из (1) при δt ≈ 10^-5 с, τ_Nb(4.2 K) ≈ 10^-12 с. Это значение близкое к оценкам Сильвера и Циммермана [1].

Рис.5 Температурная зависимость относительной энергетической щели ниобия, которая рассчитана в соответствии с теорией БКШ и экспериментальные значения щели, полученные из измерений характеристик туннельных контактов [²] (открытые небольшие квадраты) и из наших измерений импульсов напряжения V_i на контуре.

S. I. Bondarenko et al. Low Temp. Phys. 41, 179 (2015)

arXiv