Квантові інтерференційні структури для дослідження енергетичної щілини і часу релаксації надпровідного стану
С. І. Бондаренко (кер. групи), В. П. Коверя, О. В. Кревсун, В. П. Тимофеєв
Вступ
Енергетична щілина (Δ) надпровідника і час релаксації (τ) надпровідного стану є ключовими параметрами надпровідників. Енергетична щілина визначає, зокрема, максимально можливу швидкість переміщення куперівських пар і щільність критичного струму надпровідника. Час релаксації визначає максимальний високошвидкісний відгук пристроїв на основі надпровідників. Мінімізація цього параметра сприяє розвитку високочастотних і слабкострумових надпровідних пристроїв для сучасної НВЧ і обчислювальної техніки.
Основні положення методу
Ми запропонували і досліджували новий метод, який дозволяє зробити одночасні вимірювання щілини і часу релаксації. Метод об'єднує дві базові концепції. Перша з них є теоретичне передбачення Сільвера і Циммермана про те, що імпульсна напруга Vi на надпровідному квантовому інтерферометрі (НКІ) під час дискретного переключення циркулюючого струму i в ньому, який викликаний зміною магнітного потоку Фx, пропорційна енергетичній щілині надпровідника (Рис.1). Другою з них є наші пропозиції про продовження тривалості імпульсу до добре вимірюваної величини шляхом шунтування інтерферометру надпровідною котушкою з великою індуктивністю L ≈ L3 + L4 , яка значно перевищує індуктивність L0 інтерферометра (Рис.2).
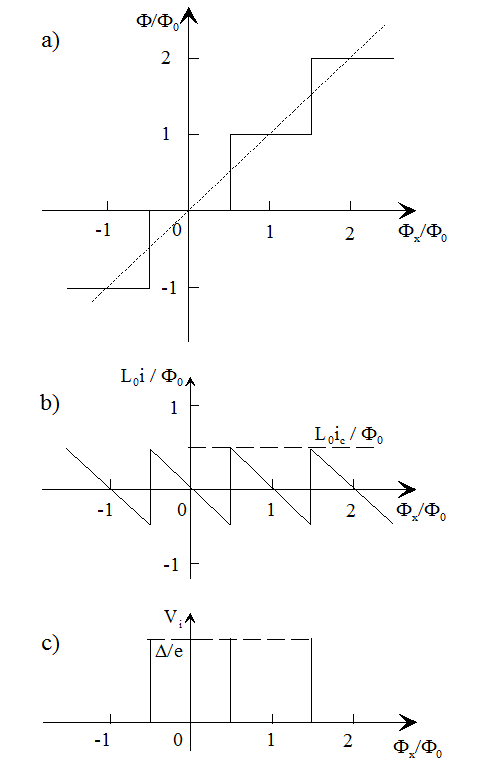
Рис.1 Розрахункова залежність відносного внутрішнього магнітного потоку Φ/Φ0 (a), відносного циркулюючого струму L0i /Ф0 (b) і імпульсної напруги Vi (c) від відносного зовнішнього магнітного потоку Фх /Ф0 , який накладається на інтерферометр з індуктивністю L0. Залежності отримані Сільвером і Циммерманом в лінійному наближенні за умови iс ≈ Ф0 /(2L0), Ф0 – квант магнітного потоку.
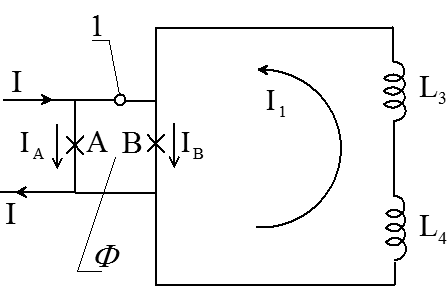
Рис.2 Електрична схема модельного контуру вимірювального пристрою, в якому притискний точковий контакт (ПТК) представлено у вигляді асиметричного НКІ (1) з двома мікроконтактами А і В, що мають різні критичні струми і включені в гілки з різними індуктивностями, Ф – магнітний потік через контур НКІ.
Вимірювання
Схему експериментальної установки для вимірювання щілини і часу релаксації представлено на Рис.3.
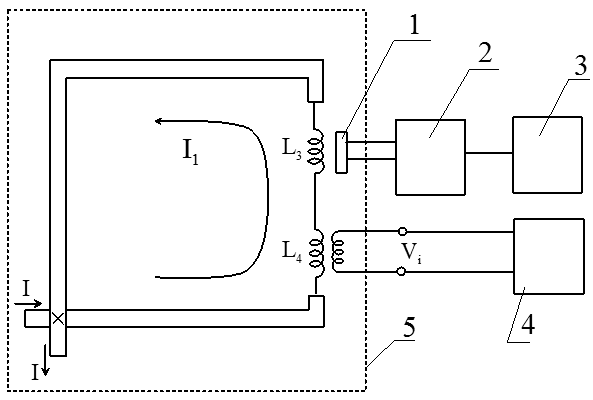
Рис.3 Вимірювальна схема для вивчення струмових станів контуру з ПТК в точці перетину (х) ніобієвих мікродротів: I – транспортний струм, 1 – ферозондовий детектор для вимірювання магнітного поля струму I1, що протікає через L3 and L4, 2 – підсилювач сигналу детектора, 3 – реєстратор виміряного магнітного поля, 4 – осцилограф для відображення і вимірювання імпульсів напруги Vi на вторинній обмотці трансформатора, які викликані дискретною зміною струму I1 через первинну обмотку із індуктивністю L4, 5 - кріостат.
Притискний точковий контакт (ПТК) ніобій-ніобій був використаний як інтерферометр. Циммерманом з колегами раніше було встановлено, що мікроструктура ПТК являє собою квантовий інтерферометр з декількома паралельно з'єднаними мікроконтактами. Зокрема, можна зробити КПК з двома мікроконтактами. Така структура являє собою надпровідний інтерферометр постійного струму (ПС) і може бути чутливим елементом, що відомий як ПС НКВІД. ПТК отримано шляхом механічного стиснення двох ніобієвих мікродротів діаметром 70 мкм, які накладені один на одного. Ніобієві дроти утворюють замкнений надпровідний контур з індуктивністю близько 10-6Гн, який включає описаний вище надпровідний інтерферометр. Інша частина контуру складається з двох котушок (L3 та L4), одна необхідна для розташування в ній детектору ферозондового магнітометру (FG) , а інша – для утворення первинної обмотки імпульсного трансформатору. Ферозонд служить для вимірювання струму в контурі. Трансформатор служить для реєстрації імпульсу напруги, що виникає в момент дискретного квантового переходу в інтерферометрі. Спочатку постійний струм I тече через ПТК, в той час як струм в гілці контуру з індуктивністю 10-6Гн практично дорівнює нулю. Інтерферометр переходить в резистивний стан із опором R за короткий час τ ≈ L0/R, як тільки досягається його критичний струм. Виникає імпульс напруги Vi на інтерферометрі і контурі, в той час як частина транспортного струму перемикається в високоіндуктивну частину контуру, що утворює струм I1 протягом часу δt ≈ L/R. Потім інтерферометр повертається до надпровідного стану. Новий дискретний перехід може відбутися в інтерферометрі після подальшого збільшення транспортного струму I , який створює магнітний потік, що дорівнює Ф0 в інтерферометрі. В результаті ми маємо залежність струму в контурі I1 від транспортному струму I , яку показано на Рис.4а. Періодичні ступені струму на залежності I1(I) відповідають квантовим переходам струму i інтерферометра, який шунтовано надпровідною індуктивністю.
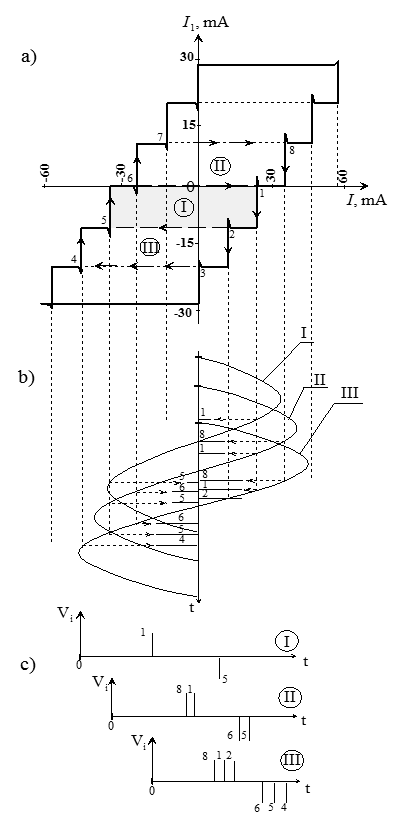
Рис.4 Схема отримання різної кількості імпульсів напруги V*i4, які спостерігаються на екрані осцилографа, коли змінний транспортний струм пропускається через контур: а) початкова експериментальна залежність I1(I) при Т = 4.2K; b) зміна змінного струму протягом одного періоду при трьох різних його амплітудах I, II, III; с) картина імпульсів напруги на екрані осцилографа (1-8 – номера ступенів струму I1, які виникають при різних амплітудах змінного струму).
Результати
Розгортка цієї залежності низькочастотним транспортним струмом (Рис.4b) дозволяє спостерігати на екрані осцилографа (Рис.4c) імпульси напруги, амплітуда яких відповідає енергетичній щілині ніобію, яка виявляється 2.3мВ при 4.2К. На Рис.5 показані експериментальні значення щілини і розрахункова крива температурної залежності щілини. Тривалість квантового переходу в інтерферометрі, тобто час релаксації надпровідного стану в ніобії, може бути оцінена із співвідношення індуктивності інтерферометра (L0 = 10-13Гн) та контуру (L = 10-6Гн):
τ ≈ (L0 / L) δt . (1)
Таким чином, як випливає з (1) при δt ≈ 10-5c, τNb(4.2K) ≈ 10-12c. Це значення близьке до оцінок Сільвера і Циммермана [1].
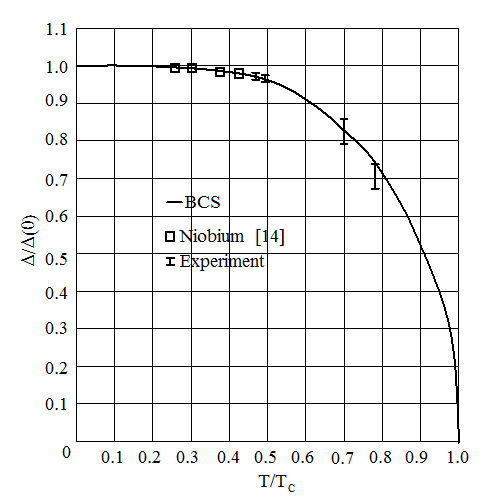
Рис.5 Температурна залежність відносної енергетичної щілини ніобію, яку розраховано відповідно до теорії БКШ і експериментальні значення щілини, отримані з вимірювань характеристик тунельних контактів [2] (відкриті невеликі квадрати) і з наших вимірювань імпульсів напруги Vi на контурі.
