DYNAMICS of QUANTUM SYSTEMS
S. N. Shevchenko (group leader), O. V. Ivakhnenko, M. P. Liul, А. I. Ryzhov, P. O. Kofman, O. Yu. Kitsenko, O. A. Ilinskaya
We study quantum dynamic phenomena in mesoscopic systems, which include superconducting circuits, low-dimensional semiconductor-based structures, nanomechanical resonators. We make use and develop the toolbox of modern condensed matter theory in order to sharpen our understanding of quantum phenomena, which are nowadays available for probing and controlling. Not only we study theoretically fundamental phenomena, such as Rabi oscillations and Landau-Zener-Stuckelberg-Majorana transitions, but we tightly relate our research to the experimental works. Recent results are outlined below, while complete list of the publications can be found at Scholar.
Optimizing Quantum Signal Processing
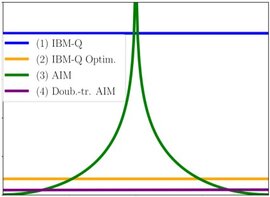
Quantum Signal Processing (QSP) is an algorithm that uses single-qubit dynamics to perform polynomial function transformation with basic unitary operations. The Adiabatic-Impulse Model (AIM) effectively describes the evolution of a two-level quantum system under an external driving field. QSP can directly use parameters from the AIM by mapping AIM’s smooth drive profiles to the phase angles in QSP, which we demonstrated: analytically, numerically (QuTiP), and using IBM-Q_Kyiv computer [1].
Modeling of the frozen zone dynamics: towards using thermal imagers in cryotherapy
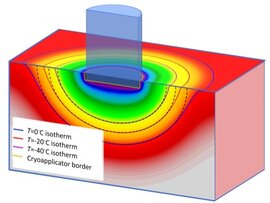 Thermal imaging for cryoablation and cryotherapy is a convenient technique, but it does not allow for visualization of what is inside. To help this, we developed a mathematical model of the temperature dynamics for materials with temperature-dependent thermodynamic parameters with a phase change boundary. Our calculations described freezing under cryoapplication both in vitro (hydrogel) and in vivo (rats, rabbits), which particularly demonstrated that the former can be used to model the latter, while thermal imagers do give information about the freezing depth [2].
Thermal imaging for cryoablation and cryotherapy is a convenient technique, but it does not allow for visualization of what is inside. To help this, we developed a mathematical model of the temperature dynamics for materials with temperature-dependent thermodynamic parameters with a phase change boundary. Our calculations described freezing under cryoapplication both in vitro (hydrogel) and in vivo (rats, rabbits), which particularly demonstrated that the former can be used to model the latter, while thermal imagers do give information about the freezing depth [2].Lecture Notes: Mesoscopic Physics meets Quantum Engineering
 The course was developed while delivering lectures to the 5th year students of the Department of Physics and Technology in Kharkov National University. Now, it is available as lecture notes, published by World Scientific. This lecture course is intended for graduate students and postdocs, who are acquainted with quantum mechanics and statistical physics. This book provides an introduction to quantum computation and quantum information, based on quantum physics, solid-state theory, and theory of computing. A reader will become familiar with this important field and explore how it is inseparably linked to basic notions of physics such as superposition, entanglement, and quantum dynamics. Then superconducting and mesoscopic systems are considered, as well as a series of phenomena, where important are the spectra quantization, interference, and charge discreteness [3].
The course was developed while delivering lectures to the 5th year students of the Department of Physics and Technology in Kharkov National University. Now, it is available as lecture notes, published by World Scientific. This lecture course is intended for graduate students and postdocs, who are acquainted with quantum mechanics and statistical physics. This book provides an introduction to quantum computation and quantum information, based on quantum physics, solid-state theory, and theory of computing. A reader will become familiar with this important field and explore how it is inseparably linked to basic notions of physics such as superposition, entanglement, and quantum dynamics. Then superconducting and mesoscopic systems are considered, as well as a series of phenomena, where important are the spectra quantization, interference, and charge discreteness [3].Landau-Zener-Stuckelberg-Majorana (LZSM) Interferometry
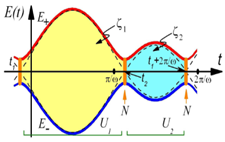
It was known since long ago that not only non-adiabatic LZSM transitions appear between discrete energy levels, but also the phase acquired during evolution matters. This phase, known as Stuckelberg phase, may result in constructive or destructive interference. We have generalized the theory to describe recently observed interference fringes in different microscopic and mesoscopic systems [4][5][6]. Such interferometry is particularly important for quantum dots [7] and superconducting structures in circuit-quantum electrodynamics [8]. We generalized and developed Majorana’s approach to validate the adiabatic-impulse approximation [9], which provides a convenient theoretical method. By investigating non-linear corrections, it was demonstrated [10] that the LZSM formula is quite robust in relation to perturbative nonlinearities, while the essential nonlinearities were treated based on the Dykhne-Davis-Pechukas formula and numerically. The LZSM physics may also provide an alternative paradigm for implementing quantum logic gates [11].
Amplitude- and Phase-Modulated Quantum Dot
 Silicon
Silicon‑based transistors can provide platform for quantum dots. We considered the impurity electron spin states in a Si tunneling field-effect transistor. The single-spin energy levels can be modulated by the radio-frequency waves. Our theoretical results, together with the experimental ones, demonstrate the potential of spin-qubit interferometry that is implemented in a Si device and is operated at relatively high temperature [12]. Furthermore, such a two-level system could provide a minimal universal quantum heat machine [13].Quantum Inductance and Capacitance
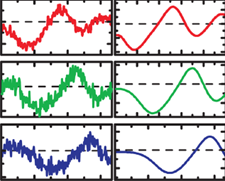 If a quantum system is included in a circuitry, it should be described in terms of the probabilities of energy level occupations. The system is then characterized by respective parametric inductances, capacitances, and resistances. Due to their dependencies on probabilities, they are also attributed the adjective “quantum”. We exploited such theory for the description of artificial few-level systems [14][15].
If a quantum system is included in a circuitry, it should be described in terms of the probabilities of energy level occupations. The system is then characterized by respective parametric inductances, capacitances, and resistances. Due to their dependencies on probabilities, they are also attributed the adjective “quantum”. We exploited such theory for the description of artificial few-level systems [14][15].See also coverage of related work in the media [16].
Mirror, mirror: a transmon qubit in a semi-infinite transmission line

We investigated the LZSM interferometry of a superconducting qubit in a semi-infinite transmission line terminated by a mirror, i.e. by a capacitor. For a probe signal, a qubit acts as another mirror, that is why we refer to our system as “mirror, mirror”. The transmon-type qubit was placed at the node of the resonant electromagnetic field, “hiding” from the field. Under the impact of the probe and dressing signals, both stationary and time-dependent states were described, in agreement with the experiment [17][18]. One of the advantages of this atom-mirror arrangement is that we can effectively manipulate the absorption properties of the artificial atom, providing a novel way to manipulate the quantum states.
Multi-Photon Transitions
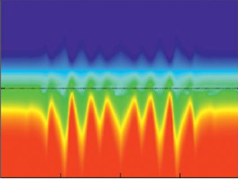 When multiple driving frequency matches the energy gap in the quantum system, this can be excited by means of the multi-photon transitions. We studied such excitations for different layouts, including single- and double-qubit systems with direct and ladder-type transitions. Even though the realistic systems are quite sophisticated – beside a quantum subsystem they include driving and controlling electronics – we succeeded in quantitative description of different driven dissipative qubit-based systems. This research resulted in the review article, the monograph, and several original papers [19][20].
When multiple driving frequency matches the energy gap in the quantum system, this can be excited by means of the multi-photon transitions. We studied such excitations for different layouts, including single- and double-qubit systems with direct and ladder-type transitions. Even though the realistic systems are quite sophisticated – beside a quantum subsystem they include driving and controlling electronics – we succeeded in quantitative description of different driven dissipative qubit-based systems. This research resulted in the review article, the monograph, and several original papers [19][20]. Thermometry with Qubit-Resonator System
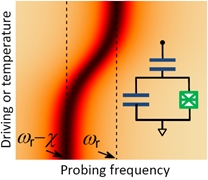 Coupled qubit and resonator present a basic system of the circuit quantum electrodynamics. We studied a qubit-resonator system subjected to both driving signal and non-zero temperature. Such consideration can be important for quantum engineering, providing description of thermometry techniques and of emergent quantum memcapacitors [21].
Coupled qubit and resonator present a basic system of the circuit quantum electrodynamics. We studied a qubit-resonator system subjected to both driving signal and non-zero temperature. Such consideration can be important for quantum engineering, providing description of thermometry techniques and of emergent quantum memcapacitors [21].Simulating Quantum Dynamics by Mechanical Resonator
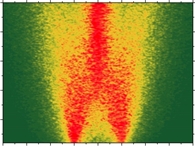
A quantum system can be driven by either sinusoidal, rectangular, or noisy signals. In the literature, these regimes are referred to as Landau-Zener-Stuckelberg-Majorana interferometry, latching modulation, and motional averaging, respectively. We demonstrate that these effects are also inherent in the dynamics of classical two-state systems. In addition to the fundamental interest of such dynamical phenomena linking classical and quantum physics, we believe that these are attractive for the classical analogue simulation of quantum systems [22].
Dynamics of Graphene Membranes
Qubit-Based Memcapacitors and Meminductors
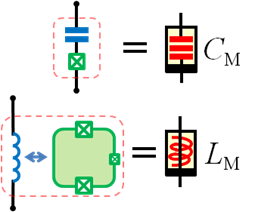 There is growing interest in electronic circuit elements that have memory; namely, memristive, memcapacitive, and meminductive circuit elements, generalizing the well-known resistors, capacitors, and inductors. We proposed and studied quantum realizations of memory circuit elements based on solid-state qubits. The quantum properties of qubit-based systems make their response unique, thus introducing a new functionality to the toolbox of memory devices [24].
There is growing interest in electronic circuit elements that have memory; namely, memristive, memcapacitive, and meminductive circuit elements, generalizing the well-known resistors, capacitors, and inductors. We proposed and studied quantum realizations of memory circuit elements based on solid-state qubits. The quantum properties of qubit-based systems make their response unique, thus introducing a new functionality to the toolbox of memory devices [24].Dressed States
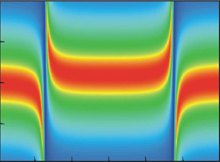 A transmission-line resonator at low temperatures behaves as quantum oscillator; its impact on coupled qubit can be described by the procedure known as dressing the qubit’s states. We developed the theory for the case of doubly-driven resonator and described the series of effects observed by the experimentalists from IPHT, Jena. It was demonstrated that such qubit-resonator system can be used for amplification or attenuation of weak signals [25][26].
A transmission-line resonator at low temperatures behaves as quantum oscillator; its impact on coupled qubit can be described by the procedure known as dressing the qubit’s states. We developed the theory for the case of doubly-driven resonator and described the series of effects observed by the experimentalists from IPHT, Jena. It was demonstrated that such qubit-resonator system can be used for amplification or attenuation of weak signals [25][26].Delayed-Response Quantum Back Action
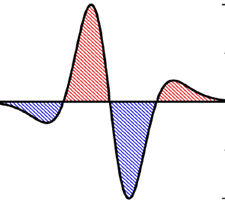 The semiclassical theory was developed for the description of the system composed of a classical resonator coupled to a quantum subsystem. Particularly, we considered the impact of the relaxation in the latter on oscillations in the former. This resulted in significantly increasing or decreasing the resonator quality factor [27][28]. We believe that our theoretical approach is useful for the description of the experiments, such as this one: [29].
The semiclassical theory was developed for the description of the system composed of a classical resonator coupled to a quantum subsystem. Particularly, we considered the impact of the relaxation in the latter on oscillations in the former. This resulted in significantly increasing or decreasing the resonator quality factor [27][28]. We believe that our theoretical approach is useful for the description of the experiments, such as this one: [29].






